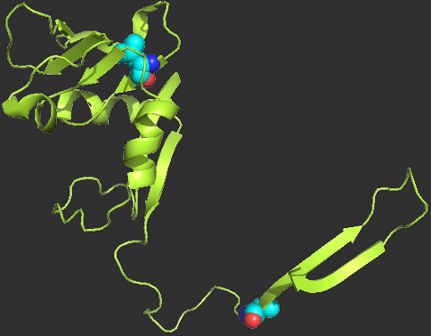
Bitran, A., Jacobs, W.M. & Shakhnovich, E. Validation of DBFOLD: An Efficient Algorithm for Computing Folding Pathways of Complex Proteins.
PLOS Computational Biology 16, 11, e1008323 (2020).
Publisher's VersionAbstractAtomistic simulations can provide valuable, experimentally-verifiable insights into protein folding mechanisms, but existing ab initio simulation methods are restricted to only the smallest proteins due to severe computational speed limits. The folding of larger proteins has been studied using native-centric potential functions, but such models omit the potentially crucial role of non-native interactions. Here, we present an algorithm, entitled DBFOLD, which can predict folding pathways for a wide range of proteins while accounting for the effects of non-native contacts. In addition, DBFOLD can predict the relative rates of different transitions within a protein's folding pathway. To accomplish this, rather than directly simulating folding, our method combines equilibrium Monte-Carlo simulations, which deploy enhanced sampling, with unfolding simulations at high temperatures. We show that under certain conditions, trajectories from these two types of simulations can be jointly analyzed to compute unknown folding rates from detailed balance. This requires inferring free energies from the equilibrium simulations, and extrapolating transition rates from the unfolding simulations to lower, physiologically-reasonable temperatures at which the native state is marginally stable. As a proof of principle, we show that our method can accurately predict folding pathways and Monte-Carlo rates for the well-characterized Streptococcal protein G. We then show that our method significantly reduces the amount of computation time required to compute the folding pathways of large, misfolding-prone proteins that lie beyond the reach of existing direct simulation. Our algorithm, which is available online, can generate detailed atomistic models of protein folding mechanisms while shedding light on the role of non-native intermediates which may crucially affect organismal fitness and are frequently implicated in disease.
Ranganathan, S. & Shakhnovich, E.I. Dynamic metastable long-living droplets formed by sticker-spacer proteins.
Elife 9, e56159 (2020).
Publisher's VersionAbstractMultivalent biopolymers phase separate into membrane-less organelles (MLOs) which exhibit liquid-like behavior. Here, we explore formation of prototypical MOs from multivalent proteins on various time and length scales and show that the kinetically arrested metastable multi-droplet state is a dynamic outcome of the interplay between two competing processes: a diffusion-limited encounter between proteins, and the exhaustion of available valencies within smaller clusters. Clusters with satisfied valencies cannot coalesce readily, resulting in metastable, long-living droplets. In the regime of dense clusters akin to phase-separation, we observe co-existing assemblies, in contrast to the single, large equilibrium-like cluster. A system-spanning network encompassing all multivalent proteins was only observed at high concentrations and large interaction valencies. In the regime favoring large clusters, we observe a slow-down in the dynamics of the condensed phase, potentially resulting in loss of function. Therefore, metastability could be a hallmark of dynamic functional droplets formed by sticker-spacer proteins.
Razban, R.M. & Shakhnovich, E.I. Effects of single mutations on protein stability are Gaussian distributed.
Biophysical Journal (2020).
Publisher's VersionAbstractThe distribution of protein stability effects is known to be well approximated by a Gaussian distribution from previous empirical fits. Starting from first-principles statistical mechanics, we more rigorously motivate this empirical observation by deriving per-residue-position protein stability effects to be Gaussian. Our derivation requires the number of amino acids to be large, which is satisfied by the standard set of 20 amino acids found in nature. No assumption is needed on the number of residues in close proximity in space, in contrast to previous applications of the central limit theorem to protein energetics. We support our derivation results with computational and experimental data on mutant protein stabilities across all types of protein residues.
Bitran, A., Jacobs, W.M., Zhai, X. & Shakhnovich, E. Cotranslational folding allows misfolding-prone proteins to circumvent deep kinetic traps.
Proceedings of the National Academy of Sciences (2020).
Publisher's VersionAbstractMany proteins must adopt a specific structure to perform their functions, and failure to do so has been linked to disease. Although small proteins often fold rapidly and spontaneously to their native conformations, larger proteins are less likely to fold correctly due to the myriad incorrect arrangements they can adopt. Here, we provide mechanistic insights into how this problem can be alleviated if proteins start folding while they are being translated by the ribosome. This process of cotranslational folding biases certain proteins away from misfolded states that tend to hinder spontaneous refolding. Signatures of unusually slow translation suggest that some of these proteins have evolved to fold cotranslationally.Many large proteins suffer from slow or inefficient folding in vitro. It has long been known that this problem can be alleviated in vivo if proteins start folding cotranslationally. However, the molecular mechanisms underlying this improvement have not been well established. To address this question, we use an all-atom simulation-based algorithm to compute the folding properties of various large protein domains as a function of nascent chain length. We find that for certain proteins, there exists a narrow window of lengths that confers both thermodynamic stability and fast folding kinetics. Beyond these lengths, folding is drastically slowed by nonnative interactions involving C-terminal residues. Thus, cotranslational folding is predicted to be beneficial because it allows proteins to take advantage of this optimal window of lengths and thus avoid kinetic traps. Interestingly, many of these proteins’ sequences contain conserved rare codons that may slow down synthesis at this optimal window, suggesting that synthesis rates may be evolutionarily tuned to optimize folding. Using kinetic modeling, we show that under certain conditions, such a slowdown indeed improves cotranslational folding efficiency by giving these nascent chains more time to fold. In contrast, other proteins are predicted not to benefit from cotranslational folding due to a lack of significant nonnative interactions, and indeed these proteins’ sequences lack conserved C-terminal rare codons. Together, these results shed light on the factors that promote proper protein folding in the cell and how biomolecular self-assembly may be optimized evolutionarily.
Chen, Q., Xiao, Y., Shakhnovich, E.I., Zhang, W. & Mu, W. Semi-rational design and molecular dynamics simulations study of the thermostability enhancement of cellobiose 2-epimerases.
International Journal of Biological Macromolecules (2020).
Publisher's VersionAbstractDirected evolution using random mutation in vast sequence space leads to the low probability of obtaining target proteins. Emerging engineering strategies with computational tools are developed for more trustable outcomes. We used some semi-rational design methods to modify an industrial enzyme, namely cellobiose 2-epimerase (CE). A mutant was selected for its better thermostability and isomerization activity. The tradeoffs between thermostability, epimerization activity and isomerization activity of the CE mutants were different. To investigate the computational prediction performance of protein stability upon point mutations, molecular dynamics (MD) simulation analyses were conducted. The root mean square deviation (RMSD) and hydrogen bond analyses reproduced the correct trends in stability changes of the wild-type and mutated CEs with relatively high accuracy (correlation coefficients r ~ 0.5–0.8). The simulation temperature and time are important factors that influence the prediction performance. Our result shows that thermostability predictors calculated from MD simulation do better in predicting the thermostability changes of the mutated enzymes than the predictors using static-state information of the enzymes.